Dave A. Alvarez, Tarra E. Fuchs, Pat L. Kirchhoeffer
Introduction
The journal article "FAST NOESY Experiments - An Approach for Fast Structure Determination" by Matthias Kock and Christian Griesinger (Angew. Chem. Int. Ed. Engl. 1994. 33. No. 3 332-334) discusses a procedure for FAST NOESY data to be manipulated so regular NOESY cross-peak integrals can be obtained. Kock and Griesinger have developed a mathematical procedure for calculating the cross-peak areas of a FAST NOESY spectrum. They use the equation:
Iij = IFij / [1-exp(-(RD + AQ) / T1j],1 {Iij = the cross peak integral of NOESY, IFij = the cross peak integral of FAST NOESY, RD = relaxation delay between scans, AQ = Acquisition Time, T1j = longitudinal relaxation times for j (determined by inversion recovery)}
In order to determine the structure of complicated molecules it is useful to obtain H,H coupling data, especially interproton distances between nearby protons. NOESY experiments allows one to obtain this data, however data collection times are necessarily long. In order to obtain good data in the past, a pause between scans equal to two or three times the longest longitudinal relaxation time (=T1=the time it takes protons to relax back to thermal equilibrium) in the molecule was required. Although many NMR procedures require a relaxation between consecutive evolution times, there is the FAST NOESY procedure in which consecutive excitation occur before complete equilibrium of the protons has occurred. FAST NOESY does not take as long as NOESY, but the integrals of these spectra are too small due to the fact that the T1 values are longer than the sum of the relaxation delay and acquisition time in the pulse sequence (see Figure A and B below). The ratio of a cross-peak FAST NOESY integral to the integral cross peak NOESY integral is less than unity [I(RD)/I(5s) < 1]. Kock and Griesinger have discovered a mathematical way to compensate for the weak peaks of a FAST NOESY. They derived their equation for the Liouville-von-Neuman equation, which provides exact correction of NOESY spectra, including spin diffusion effects.2
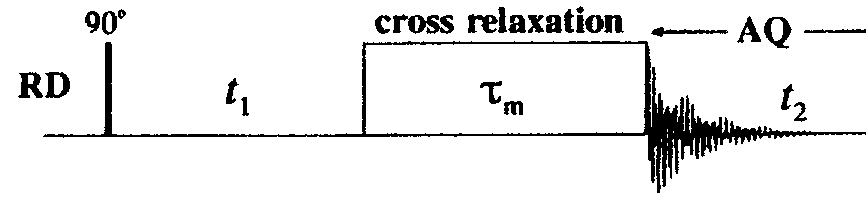
Figure A1
The pulse sequence for NOESY

Figure B1 The two plots at the top are NOESY spectra of the compound shown in Fig. C below (where RD = 5 sec). The two plots at the bottom are FAST NOESY spectra of compound C (where RD = 0.25 sec). [NOESY between protons 10 proS, 15 proR, 12 and 13 are shown]
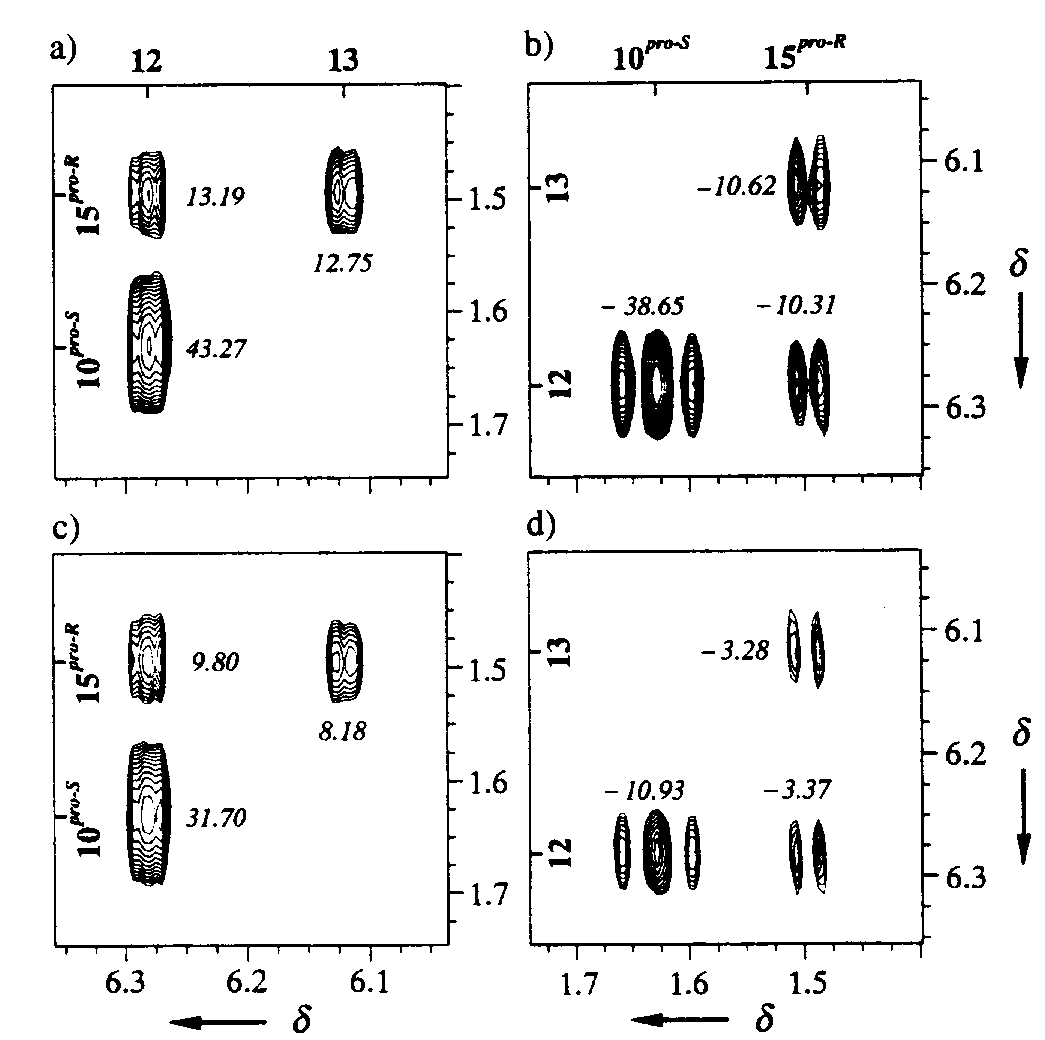
Figure C1 A complex organic molecule C25H26NO4S
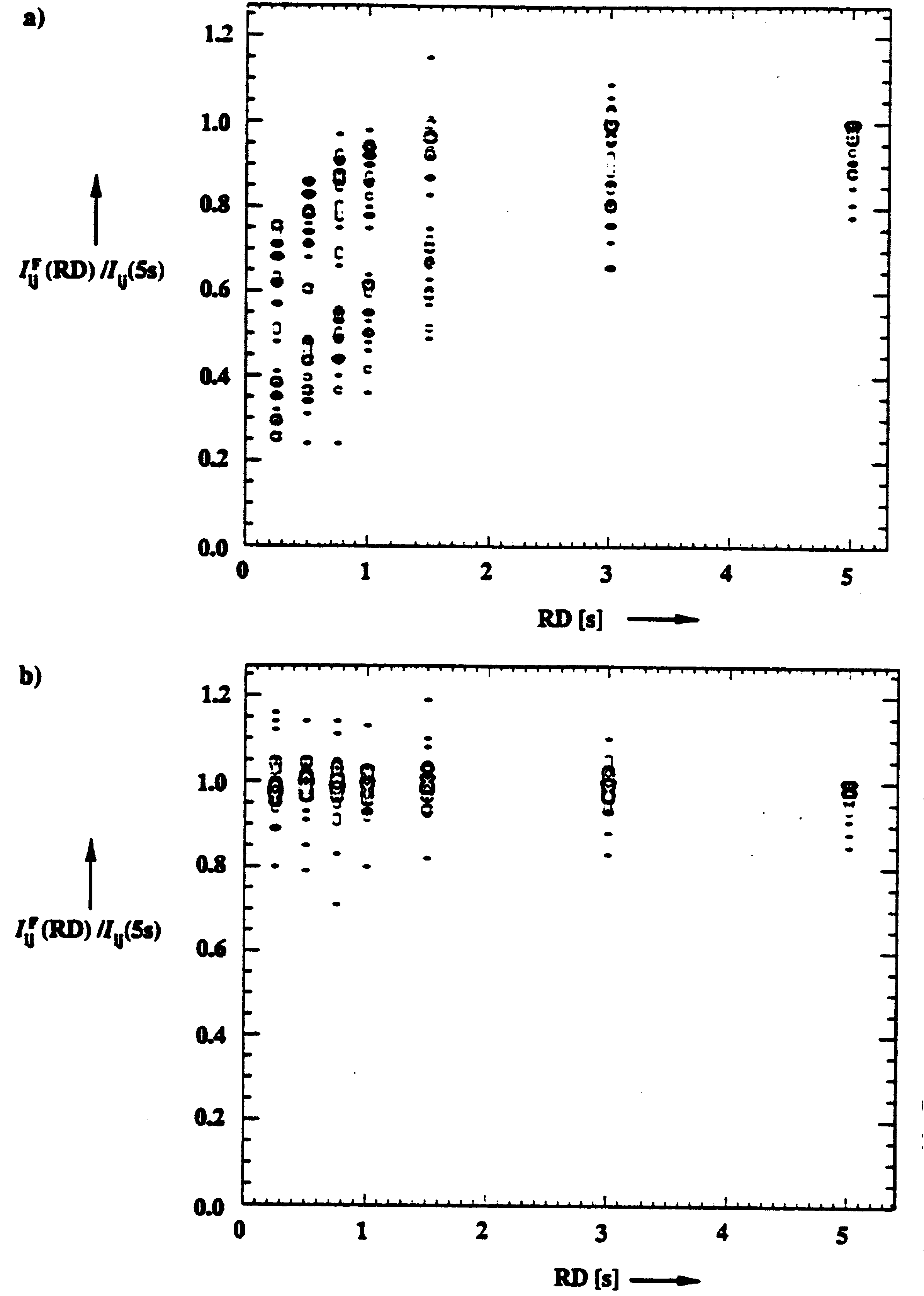
Figure D1 Integral ratios of FAST NOESY: NOESY vs.RD. Data obtained for comparison was from the compound in Fig C. 46 cross peak integrals were evaluated.
Questions
1. Using the notations from the structure of the molecule in Fig. C, determine the spectra of the H NMR for T6,T5, and T7 using the increment system from Pretch et al.3 Then draw a 2D-COSY spectra, making sure to show the coupling between protons. {category FAR}.
2. One of the main concepts of this article is cross relaxation. Explain in detail what cross relaxation is and the importance of it in NOESY spectra. (see the article1 and any NMR book for help) {category ICR}
3. Before you can understand NOESY, you first must know what NOE is. Using both words and diagrams explain the Nuclear Overhauser Effect in terms of the two spin system AX.(see Friebolin4 for help) {category SCL}
4. Discuss the advantages and disadvantages of FAST NOESY over normal NOESY when using 2D NMR to aid in structural determination. (using Figure C and the actual article1 may help) {category ICR}
5. Figure D shows the integral cross-peak ratios (IFAST/INOESY) plotted against the FAST NOESY relaxation delay (RD). Plot a shows the ratios resulting from uncorrected FAST NOESY integral values. Plot (b) shows ratios resulting from the corrected FAST NOESY integral values. Discuss the significance between the two plots. {category RQD}
References
[1] Kock, M.; Griesinger, C. Angew. Chem. Int. Ed. Engl. 1994, 33, 332-334.
[2] Ernst, R. R.; Bodenhausen, G.; Wokaun, A. Principles of Nuclear Magnetic Resonance in One and Two Dimensions; Clarendon Press: New York, Oxford, 1987.
[3] Pretsch; Clerc; Seibl; Simon Tables of Spectral Data for Structure Determination of Organic Compounds; Fresenius, W. et al., Ed.; Springer-Verlag: Berlin, Heidelberg, 1989.
[4] Friebolin, H. Basic One- and Two-Dimensional NMR Spectroscopy; 2nd Ed. VCH: New York, NY, 1993.